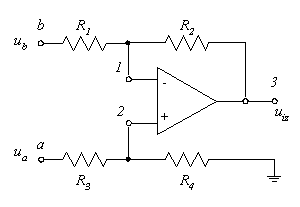
3.2.3 Diferencijalno pojačalo

Operaciono pojačalo povezano na način prikazan na slici 3.2-3 naziva se opterećenim pojačalom. Opterećenost pojačala se odnosi na činjenicu da izlazni napon ima oblik u_iz = w_au_a + w_bu_b, pri čemu su težinski koeficijenti, w_a i w_b, naponska pojačanja gledana sa strane ulaza. Analiza sklopa je jednostavna. Budući se vrijednosti izlaznog i ulaznih napona nalaze u linearnom odnosu u analizi je dozvoljeno primijeniti princip superpozicije.

Slika 3.2-3 Osnovno diferencijalno pojačalo

U prvom slučaju, neka je u_a = 0. Uvjet se postiže uzemljenjem ulazne stezaljke grane otpora R₃. U tom slučaju su između stezaljke 2 i zajedničke točke otpori R₃ i R₄ paralelno spojeni i potencijal stezaljke 2 je nula. Sklop promatran sa ulaza u_b, predstavlja invertirajuće pojačalo s pojačanjem -R₂/R₁. Budući struja ne teče u stezaljku 2, otpornici R₃ i R₄ ne djeluju na sklop, te je

                                                                                                                (3.2-5)

U drugom slučaju, neka je u_b = 0, što odgovara uzemljenju ulazne stezaljke grane otpora R₁. Sklop promatran s ulaza u_b predstavlja neinvertirajuće pojačalo pojačanja [ 1 + (R₂ /R₁)] . Budući djelitelj napona sastavljen od otpornika R₃ i R₄ daje vrijednost R₄/( R₃ + R₄) promatran sa stezaljke 2, izraz za w_a glasi

                                                                                                 (3.2-6)

Konačno, ukupni odziv slijedi superpozicijom

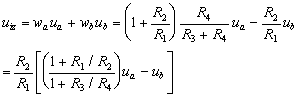                                                                  (3.2-7)

U posebnom slučaju kada je

                                                                                                                  (3.2-8)

odziv odgovara odzivu diferencijalnog pojačala

                                                                                                        (3.2-9)

Radi praktičnih razloga diferencijalno pojačalo se obično izvodi s R₃ = R₁ i R₄ = R₂.

U slučaju velikog iznosa pojačanja diferencijalnog pojačala ulazni otpor je mali, što dovodi do male vrijednosti R₁. Nepovoljan utjecaj velikih i nejednakih iznosa unutarnjih otpora izvora u_a i u_b smanjuje se postavljanjem visokog ulaznog otpora neinvertirajućeg pojačala, slika 3.2-4.

Slika 3.2-4 Diferencijalno pojačalo

U tom slučaju odziv glasi

                                                                                        (3.2-10)

povratak